008 Sequências - Exercícios Comentados

1) (2012 - CETRO) Considere a sequência de retângulos com os respectivos números e letras (alfabeto de 23 letras) que obedecem a uma lei de formação.


A)

B)

C)

D)


A sequência de letras segue a ordem inversa do alfabeto e vai progressivamente pulando letras.
A sequência de números segue ordem decrescente, o valor subtraído são números ímpares em ordem crescente.

---

2) (2013 - CETRO) O próximo valor correto para a sequência 0, 6, 24,... é
A) 78.
B) 66.
C) 58.
D) 48.
E) 46.

Questão muito difícil, pois há poucos termos e definir uma regra válida para todos não é fácil.
Acredito que o examinador pretendeu [tex]A_{n}=-3+3^{n}[/tex].

[tex]A_{1}=-3+3^{1}[/tex]
[tex]A_{1}=-3+3=0[/tex]

[tex]A_{2}=-3+3^{2}[/tex]
[tex]A_{2}=-3+9=6[/tex]

[tex]A_{3}=-3+3^{3}[/tex]
[tex]A_{3}=-3+27=24[/tex]

[tex]A_{3}=-3+3^{4}[/tex]
[tex]A_{3}=-3+81=78[/tex]

Nada óbvio.

O pior é que com criatividade é possível chegar a outro resultado. Tome por exemplo, a "função dos divisores", sigma, que associa a cada número natural n a soma de seus divisores naturais elevados à potência k.

[tex]\sigma _{k}(n)=\sum_{d|n}d^{k}[/tex]

[tex]\sigma _{1}(1)=1[/tex] é a soma dos números naturais que dividem 1 elevados à potência 1.

[tex]\sigma _{2}(2)=1^{2}+2^{2}[/tex] é a soma dos divisores de 2 elevados à potência 2.

[tex]\sigma _{1}(3)=1+3[/tex] é a soma dos divisores de 3 elevados à potência 1.

[tex]\sigma _{1}(4)=1+2+4[/tex] é a soma dos divisores de 4 elevados à potência 1.

[tex]\sigma _{3}(6)=1^{3}+2^{3}+3^{3}+6^{3}[/tex] é a soma dos divisores de 6 elevados à potência 3.


Segue que a sequência do enunciado poderia ser definida como:

[tex]A_{n}=\sigma _{3}(n)-\sigma _{1}(n)[/tex]

[tex]A_{1}=\sigma _{3}(1)-\sigma _{1}(1)=1^{3}-1=0[/tex]

[tex]A_{2}=\sigma _{3}(2)-\sigma _{1}(2)=1^{3}+2^{3}-(1+2)=6[/tex]

[tex]A_{3}=\sigma _{3}(3)-\sigma _{1}(3)=1^{3}+3^{3}-(1+3)3=24[/tex]

[tex]A_{4}=\sigma _{3}(4)-\sigma _{1}(4)=1^{3}+2^{3}+4^{3}-(1+2+4)=66[/tex]

Letra B seria a resposta para essa função.
Viagem? Sim, mas é possível, afinal é uma função que gera os três primeiros termos.

---

3) (2013 - FGV) Em um depósito há apenas bolsas de sangue dos tipos sanguíneos A e O armazenadas em sequência conforme sugerido a seguir:

A2572, A2573, A2574, ..., A2821
O1878, O1879, O1880, ..., O2013

Sabe-se que cada uma das duas sequências segue a ordem dos números naturais sem faltas ou multiplicidades.

A quantidade de bolsas de sangue nesse depósito é
A) 384.
B) 385.
C) 386.
D) 387.
E) 388.

Se você tivesse artigos numerados de 1 a 20, você teria 20 artigos. É fácil contar assim.
Para que a bolsa de sangue A2572 seja a número A1, é necessário subtrair 2571.
2572 - 2571 = 1
2821 - 2571 = 250
Agora as bolsas estão numeradas de A1 a A250.

Faça o mesmo para as bolsas com sangue O.
1878 - 1877 = 1
2013 - 1877 = 136
Agora as bolsas estão numeradas de O1 a O136

Ao todo são 336 bolsas de sangue.

---

4) (2015 - FCC) Em uma sequência de números inteiros, o primeiro elemento vale 1 e o segundo elemento vale - 1. A partir do terceiro, cada elemento é igual ao produto dos dois elementos imediatamente anteriores a ele. A soma dos primeiros 2015 elementos dessa sequência é igual a
A) -671.
B) -673.
C) -1.
D) -2013.
E) -2015.

O produto é sinônimo de multiplicação entre os elementos.
Os dois primeiros termos são 1 e -1.
A sequência vai seguir o padrão 1, -1, -1, 1, -1, -1, 1, -1, -1, 1, -1, -1, ...
Dá para perceber que um trio de elementos forma um padrão que se repete ao longo da sequência: (1, -1, -1), (1, -1, -1), (1, -1, -1), (1, -1, -1), ...
Em 2015 termos esse padrão vai aparecer 2015/3 = 617 vezes e ainda sobrarão 2 elementos.
O saldo de cada padrão é igual a 1-1-1 = -1.
Portanto, a soma dos 617 padrões é igual a -617.
A soma dos 2 elementos restantes é igual 1-1 = 0.

---

5) (2014 - VUNESP) As pastas de um arquivo são nomeadas com 4 caracteres alfanuméricos da seguinte maneira:

1.º caractere: uma letra escolhida entre {L, M, N, P, Q, R, S, T, U}
2.º caractere: um algarismo escolhido entre {0, 1, 2, 3, 4, 5}
3.º caractere: uma letra escolhida entre {A, B, C, D, E, F, G, H, J, K, L}
4.º caractere: um algarismo escolhido entre {2, 3, 4, 5, 6, 7}

Cada pasta tem um nome único e todas as pastas estão ordenadas de maneira que a pasta L0A2 é a primeira, L0A3, a segunda, seguindo a ordem alfabética e numérica, até a última pasta, de nome U5L7. Seguindo esse padrão, a pasta de nome R2D2 ocupa a posição
A) 2 000.
B) 2 131.
C) 2 222.
D) 2 323.
E) 2 456.

O jeito é verificar o número de permutações possíveis até chegar em R2D2.

Imagine 4 casas para representar os 4 caracteres. _ * _ * _ * _ A primeira casa contém o primeiro caractere, mas queremos apenas os que antecedem R2D2, então restringimos a primeira casa para começar por uma letra entre {L, M, N, P, Q).
5 * _ * _ * _

A segunda casa pode ser preenchida com qualquer um dos 6 caracteres disponíveis para a segunda posição.
5 * 6 * _ * _

E assim por diante.
Há 5 * 6 * 11 * 6 permutações possíveis, ou seja, 1980 permutações.

Para o primeiro caractere sendo igual a R e o segundo sendo {0, 1} há
1 * 2 * 11 * 6 permutações, isto é, 132.

Para o primeiro caractere sendo igual a R e o segundo sendo 2 e o terceiro sendo igual a {A, B, C} há
1 * 1 * 3 * 6 permutações que é igual a 18

1980 + 132 + 18 = 2130 permutações de L0A1 a R2C7.
A próxima pasta é a R2D2.

---

6) (2012 - CESGRANRIO)

Na figura mostrada acima, um retângulo de lados 4 cm e 7 cm foi dividido em quadrados cujos lados medem 1 cm. Ao traçar uma diagonal do retângulo observa-se que, ela intercepta os lados de exatamente 10 quadrados, como ressaltado na figura.
Se o retângulo fosse dividido em quadrados de lado medindo 0,5 cm, a diagonal interceptaria os lados de quantos quadrados?

Obs.:Considere que o vértice faz parte do lado do quadrado.
A) 40
B) 22
C) 18
D) 10
E) 5

Se as dimensões dos quadrados passarem de 1 x 1 cm² para 0,5 x 0,5 cm², a grade terá 4 vezes o número de quadrados originais.
A reta atravessará o dobro do número de quadrados anteriores. Porém, no centro, a linha cruzará os quadrados bem no vértice. Portanto os quatro quadrados do centro são interceptados pela reta.
Ao todo são 20 + 2 quadrados interceptados.

---

7) (2015 - UPENET/IAUPE) Considerando o alfabeto com 26 letras e a regra de formação da sequência abaixo, quais as duas próximas letras que completam a sequência [A E C G E I G K I ...]
A) K O
B) J I
C) G M
D) M K
E) L N

A sequência pode ser dividida em duas listas em ordem alfabética que pulam sempre uma letra:
A _ C _ E _ G _ I _ ?
_ E _ G _ I _ K _ ?

Comepletando os espaços em branco:
A B C D E F G H I J K
D E F G H I J K L M

A primeira letra segue a sequência de baixo e será a letra M.
A segunda letra segue a sequência de cima e será a letra K.
Resposta: letra D.

---

8) (2012 - IF-SP) Qual é o próximo número da sequência 2, 3, 5, 9, 17,...?
A) 19
B) 33
C) 25
D) 31
E) 29

O valor somado é duplicado em cada termo subsequente. Os valores somados são 1, 2, 4, 8 e 16 ...
2 + 1 = 3
3 + 2 = 5
5 + 4 = 9
9 + 8 = 17
17 + 16 = 33

---

9) (2012 - Cetro) Assinale a alternativa que substitui corretamente o ponto de interrogação na sequência abaixo.
51, 61, 153, 183, 459, 549, ?
A) 627.
B) 787.
C) 957.
D) 1377.
E) 1647.

ão duas sequências intrelaçadas que seguem a mesma regra de formação. A primeira sequência começa com 51 e a segunda com 61. O próximo termo de cada sequência é três vezes superior ao anterior:

51, __, 153, ___, 459, ___ , ?
__, 61, ___, 183, ___, 549

51 * 3 = 153
153 * 3 = 459
459 * 3 = 1377

10) (2015 - IADES) A sequência numérica (17, 15, 13, ...) foi montada, a partir do segundo termo, somando-se 8 ao algarismo das unidades do termo anterior. Nessas condições, a soma dos algarismos do número que ocupa a 834a posição na sequência é
A) 2.
B) 4.
C) 6.
D) 8.
E) 9.

Pela lógica do enunciado, somente a casa das unidade muda enquanto que a da dezena permanece constante. Os termos vão aparecer de forma cíclica em intervalos de cinco termos.
(17, 15, 13, 11, 19), (17, 15, 13, 11, 19), (17, 15, 13, ...

Ao dividir 834 por 5, obtemos um quociente de 166 e resto igual a 4.

O quociente indica que o ciclo de cinco termos ocorreu de forma completa 166 vezes até o 843º termo.
Após completar o 166º ciclo, restam 4 termos para chegar ao 834º termo. Por isso, o resto 4 significa que o 834º termo é igual ao quarto termo da sequência, 11.
Ao somarmos os dois dígitos do quarto termo da sequência obtém-se 2.

A letra A responde à questão.

---

Prova 2016 - CESGRANRIO - IBGE - Agente de Pesquisa e Mapeamento - RLM Comentada

1) O setor de uma empresa enviou os seus 10 funcionários para participarem de um curso sobre a utilização de um sistema de preenchimento de relatórios. Ao final do curso, todos os funcionários passaram a utilizar o sistema no mesmo ritmo, isto é, cada um passou a preencher a mesma quantidade de relatórios por hora: cada 4 funcionários preenchem 48 relatórios em 6 horas.
Após o curso, em quantas horas 8 funcionários preencheriam 96 relatórios?
(A) 6
(B) 4
(C) 3
(D) 12
(E) 8

O problema quer saber a quantidade de horas.
Pode-se resolver o problema por meio da regra de três composta.

Funcionários	Relatórios	Horas
4	48	6
8	96	x

Primeiro passo é organizar os valores em forma de equação. A incógnita x sempre deve ficar só em um dos lados da equação.
Os valores da fileira de baixo serão os numeradores das frações e os valores da fileira de cima serão os denominadores.

[tex]\frac{x}{6}=\frac{96}{48}*\frac{8}{4}[/tex]

O segundo passo é inverter o numerador e denominador das frações em que a grandeza seja inversamente proporcional em relação a  grandeza de x.

Pergunte: "Se aumentar o número de horas, é necessário mais ou menos funcionários para produzir uma mesma quantidade de relatórios?"
São necessários menos funcionários, para mais horas. O número de horas e número de funcionários são grandezas inversamente proporcionais.

Pergunte: "Se aumentar o número de horas, produzem-se mais ou menos relatórios em um mesmo lapso temporal?"
Produzem-se mais relatórios, para mais horas. O número de horas e quantidade de relatórios são diretamente proporcionais.

Invertem-se o numerador e o denominador da fração referente a relatórios:

[tex]\frac{x}{6}=\frac{48}{96}*\frac{8}{4}[/tex]

Simplifique e resolva:

[tex]\frac{x}{6}=\frac{1}{2}*2[/tex]

[tex]\frac{x}{6}=1[/tex]

[tex]x=6[/tex] horas

Letra A

---

2) Maria disse que sua família possui um único carro.
Se Maria mentiu, então a sua família
(A) possui mais de um carro.
(B) possui outro tipo de veículo.
(C) não possui carro, ou possui mais de um carro.
(D) não possui carro.
(E) não gosta de carros.

Para negar a afirmação de Maria, é necessário que a família possua uma quantidade de carros diferente de 1.

Pode ser que a família de Maria possua mais de um carro ou pode ser que a família de Maria não possa carro algum.
Em ambos os casos Maria estaria mentindo.

A letra C cobre esses dois casos.

---

3) Considere as seguintes definições:
1 - Um triângulo é chamado de escaleno quando os seus lados possuem comprimentos diferentes.
2 - Um triângulo é chamado de isósceles quando há dois de seus lados com o mesmo comprimento.
3 - Um triângulo é chamado de equilátero quando todos os seus lados possuem o mesmo comprimento.
De acordo com as definições apresentadas, um triângulo não é escaleno quando, e apenas quando, ele
(A) não é equilátero.
(B) não é isósceles.
(C) é isósceles.
(D) é isósceles, mas não é equilátero.
(E) não é equilátero, nem é isósceles.

De forma simplificada: "Se todos os lados são diferentes, então o triângulo é escaleno".

A contrapositiva dessa afirmativa é: "Se o triângulo não é escaleno, então existem pelo menos dois lados iguais".

Segue que, se um triângulo não é escaleno, então o triângulo é isósceles ou equilátero.

O enunciado não deixa muito claro, mas todo triângulo equilátero é isósceles, visto que há pelo menos dois lados iguais.

Conclui-se que todo triângulo não escaleno é isósceles.

Letra C.

---

4) Considere a seguinte argumentação:
Se alguém tivesse faltado à festa, então todos teriam passado por interesseiros.
No entanto, alguém não passou por interesseiro.
Conclui-se que
(A) ninguém faltou à festa.
(B) quem faltou à festa é interesseiro.
(C) alguém foi à festa, mas não todos.
(D) não houve festa.
(E) todos faltaram à festa.

Proposições:
P = Alguém faltou à festa.
~P = Ninguém faltou à festa / Todos foram à festa.
Q = Todos passaram por interesseiros.
~Q = Alguém não passou por interesseiro.

Premissa 1: P→Q
Premissa 2: ~Q
Conclusão: ~P (Modus Tollens)

Letra A.

---

5) Todos os funcionários de uma empresa encerram suas atividades às 18h e seguem para suas casas usando ônibus ou van. Os funcionários que usam ônibus seguem até a rodoviária e lá pegam outro ônibus ou um táxi. Os funcionários que usam a van seguem até a zona portuária e lá pegam as barcas.
Portanto, os funcionários que não usam táxi para seguirem para suas casas, após encerrarem suas atividades,
(A) não usam van, se usarem a barca.
(B) não usam barca, mas usam van.
(C) não usam ônibus.
(D) usam ônibus, se não usarem a barca.
(E) usam ônibus, mas não usam a barca.

As opções para voltar para casa são:
Ônibus seguido por outro ônibus ou por táxi.
OU
Van seguida por barca.

Os funcionários que não usam táxi são os que voltam por um dos seguintes percursos:
Ônibus seguido por outro ônibus.
OU
Van seguida por barca.

A letra A está errada, pois se usarem barca é porque usaram van. Além do que, não é uma conclusão completa, pois pode ser que usem ônibus.

A letra B está errada, pois se usam van, usam barca também. Além do que, não é uma conclusão completa, pois pode ser que usem ônibus.

A letra C está errada, pois pode ser que usem ônibus, sim.

A letra E está errada, pois não é necessário que usem ônibus e pode ser que usem barca.

A letra D está certa. Se não usarem a barca, então esses funcionários voltaram para casa usando os dois ônibus.

---

6) Cinco amigos passaram o final de semana juntos em uma pousada. O valor total da conta foi de R$ 3.720,40, e cada um pagou apenas a parte que lhe cabia, dentre as despesas de hospedagem, passeios e frigobar.
É necessariamente verdade que
(A) algum amigo gastou entre R$ 744,00 e R$ 745,00.
(B) algum amigo gastou menos do que R$ 744,00.
(C) algum amigo gastou mais do que R$ 744,05.
(D) cada amigo gastou mais do que R$ 740,05.
(E) cada amigo gastou menos do que R$ 745,00.

Para resolver esse tipo de problema é necessário encontrar ao menos uma hipótese que contradiga a assertiva. Caso seja impossível contradizê-la, então necessariamente a assertiva está correta.

A letra A está errada porque pode ser que os custos de hospedagem e alimentação tivessem inclusos, mas um amigo resolveu comprar um artigo caro fora do pacote e pagou sozinho R$ 3.720,40. Nesse caso, nenhum dos amigos teria gasto um valor entre 744 e 745 reais.

A letra B está errada, porque 744 * 5 = 3720 e esse valor é inferior a 3720,40 em 40 centavos.
Portanto é possível que 4 amigos tenham pago 744,00 e o outro pagou 744,40, caso este em que nenhum amigo gastou menos do que R$ 744,00.

A letra D está errada pelo mesmo motivo que a letra A. É possível que apenas um dos amigos arcou com o gasto total e, portanto, houve quatro pessoas que não gastaram mais do que R$ 740,05.

A letra E está errada pelo mesmo motivo que a letra A. É possível que alguém tenha pago o valor cheio e, portanto, pagou mais do que R$ 745,00.

A letra C está certa já que 744,05 * 5 = 3.720,25.
Como 3.720,25 é inferior a 3.720,40, então pelo menos um dos cinco amigos teve que arcar com os quinze centavos restante e necessariamente pagou um valor acima R$ 744,05.

---

7) A Figura mostra as cinco etapas seguidas para se dobrar uma folha de papel, conforme disposta inicialmente na etapa 1. Foram feitas duas dobras, nas etapas 2 e 4, ao longo dos segmentos tracejados, que dividem ao meio a folha presente nas etapas 1 e 3, respectivamente.




Na etapa 5, no local indicado pelo ponto, a folha dobrada foi atravessada perpendicularmente por um lápis, sendo feito um furo de lado a lado.

Se a folha for desdobrada e retornar à forma disposta na etapa 1, então qual a representação correta da disposição dos furos obtidos?

(A)

(B)

(C)

(D)

(E)


Só não vá fazer o experimento no seu caderno de prova, huh?

Tente visualizar as etapas de trás para frente.

---

8) Na Figura a seguir, PQ mede 6 cm, QR mede 12 cm, RS mede 9 cm, e ST mede 4 cm.

A distância entre os pontos P e T, em cm, mede
(A) 19
(B) 18
(C) 17
(D) 21
(E) 20

As medidas que o enunciado informa são


Faça com que a diagonal PT seja igual à hipotenusa de um triângulo com base e altura conhecidos:


Base = 15 cm (PQ + RS).
Altura = 8 cm (QR - ST).

Aplicando o Teorema de Pitágoras:

[tex]Base^{2}+Altura^{2}=Hipotenusa^{2}[/tex]

[tex]15^{2}+8^{2}=PT^{2}[/tex]

[tex]15^{2}+8^{2}=PT^{2}[/tex]

[tex]225+64=PT^{2}[/tex]

[tex]PT=\sqrt{289}[/tex]

[tex]PT=17[/tex]

Letra C.

---

9) Considere cinco punhados idênticos de feijões, ou seja, com a mesma quantidade de feijão. Tais punhados estão enfileirados e numerados do primeiro ao quinto. Uma pessoa retira de cada punhado, exceto do terceiro, três feijões e os coloca no terceiro punhado. Em seguida, essa pessoa retira do terceiro punhado tantos feijões quantos restaram no segundo e os coloca no primeiro punhado.
Após os procedimentos realizados por essa pessoa, quantos feijões sobraram no terceiro punhado?
(A) 10
(B) 9
(C) 7
(D) 15
(E) 12

Cada punhado tem inicialmente X feijões.
A pessoa retirou 3 feijões dos punhados, exceto do terceiro, e os colocou nesse.

Após o procedimento, o terceiro punhado ficou com X+12 feijões.
Os demais punhados ficaram com X-3 feijões.

Em seguida, a pessoa retira X-3 feijões do terceiro punhado e os coloca no primeiro.
Quantos restam no terceiro punhado?
Resto = X + 12 - (X-3)
Resto = X + 12 - X + 3
Resto = 15

Letra D.

---

10) Em cada jogo de um torneio de futebol, um time pode vencer, se fizer mais gols que o adversário, empatar, se fizer o mesmo número de gols que o adversário, ou perder, se fizer menos gols que seu adversário.
Um determinado time de futebol jogou três partidas e ficou com saldo de gols positivo, ou seja, fez mais gols do que sofreu.
Qual das campanhas a seguir NÃO pode ter sido a campanha do time citado?
(A) 1 Vitória, 1 Derrota e 1 Empate
(B) 0 Vitória, 1 Derrota e 2 Empates
(C) 1 Vitória, 0 Derrota e 2 Empates
(D) 2 Vitórias, 0 Derrota e 1 Empate
(E) 1 Vitória, 2 Derrotas e 0 Empate

Uma vitória significa um saldo positivo de gols.
Um empate significa um saldo nulo.
Uma derrota significa um saldo negativo.

As letras A, C, D e E podem ter sido a campanha. Basta que o saldo positivo das vitórias supere o saldo negativo das derrotas.

A letra B não pode ter sido a campanha do time. Não é possível um saldo positivo após sofrer 1 derrota e 2 empates, pois derrotas são saldos negativos e empates nulos.

---

11) Antes da final do Novo Basquete Brasil, 9 pessoas foram convidadas a participar de uma apresentação na qual cada uma delas faria 8 arremessos livres à cesta. Dentre essas pessoas havia alguns profissionais, e o restante era composto de torcedores que foram escolhidos aleatoriamente. Os números de arremessos convertidos pelos participantes foram: 1, 2, 2, 3, 4, 5, 5, 6 e 7. Nenhum torcedor acertou mais arremessos do que qualquer um dos profissionais. Apenas 2 torcedores converteram o mesmo número de arremessos, e um torcedor converteu o mesmo número de arremessos que um profissional.
Quantos profissionais foram convidados para a apresentação?
(A) 5
(B) 6
(C) 7
(D) 3
(E) 4

Um torcedor converteu o mesmo número de arremessos que um profissional.
Há dois pares de pontuações iguais: 2, 2 e 5, 5.
Um desses pares é compartilhado por um torcedor e um profissional. O outro pode ser o arremesso de dois profissionais ou de dois amadores.

Nenhum torcedor acertou mais arremessos do que qualquer um dos profissionais.
Pode ser que haja sete profissionais. Os torcedores teriam convertido 1 e 2, enquanto que os profissionais tenham convertido 2, 3, 4, 5, 5, 6 e 7.
Pode ser que haja três profissionais. Os torcedores tenham convertido 1, 2, 2, 3, 4 e 5 e os profissionais tenham convertido 5, 6 e 7.

Finalmente, Apenas 2 torcedores converteram o mesmo número de arremessos. Então, não é possível que os torcedores tenham convertido 1 e 2.
É necessário que eles tenham convertido 1, 2, 2, 3, 4 e 5 de modo que dois torcedores converteram a mesma pontuação: 2 e 2.

Conclui-se a partir das informações que há 3 profissionais.

Letra D.

---

12) A Figura a seguir mostra as flores de um canteiro, e o número abaixo de cada flor representa a quantidade, em mg, de pólen de cada uma das flores.

Uma abelha visita esse canteiro para colher pólen, mas consegue carregar, no máximo, 8 mg de pólen por viagem. Sabe-se ainda que, em cada viagem, a abelha colhe o pólen de uma única flor, que pode ser revisitada em outras viagens.
Qual a quantidade máxima de pólen, em mg, que essa abelha consegue colher em 24 viagens?
(A) 190
(B) 184
(C) 180
(D) 192
(E) 191

O ideal é que a abelha tente sempre carregar o máximo de pólen possível em cada viagem. Para tanto, a abelha sempre deve escolher uma flor que tenha pelo menos 8 mg de pólen.

Uma divisão por 8 nos informa quantas visitas a abelha consegue fazer a cada flor antes de restar uma quantidade de pólen inferior a 8 mg.

Por exemplo, para a flor com 52 mg a abelha pode fazer 52/8=6 visitas e restará 4 mg de pólen.

Pólen Inicial	Número de visitas	Resto da divisão
6	6/8 = 0	6 mg
52	52/8 = 6	4 mg
35	35/8=4	3 mg
82	82/8=10	2 mg
23	23/8=2	7 mg
11	11/8=1	3 mg

Somando o número total de visitas em que a abelha carrega o máximo de pólen possível:
0 + 6 + 4 + 10 + 2 + 1 = 23 visitas.

Na última viagem a abelha deve escolher a flor que ficou com mais pólen, isto é, a flor que ficou com 7 mg.

Ao todo ela consegue captar (23*8) + 7 = 187 + 7 = 191 mg de pólen.

Letra E.

---

13) Em uma prova de múltipla escolha, todas as questões tinham o mesmo peso, ou seja, a cada questão foi atribuído o mesmo valor. Aldo tirou nota 5 nessa prova, o que corresponde a acertar 50% das questões da prova. Ao conferir suas marcações com o gabarito da prova, Aldo verificou que acertou 13 das 20 primeiras questões, mas constatou que havia acertado apenas 25% das restantes.
Quantas questões tinha a prova?
(A) 52
(B) 32
(C) 24
(D) 84
(E) 72

O restante da prova tinha X questões, das quais Aldo acertou 25%, ou seja, 1/4 de X.
Ao todo ele acertou 13 + 0,25X questões.
A prova tinha 20 + X itens.

Como ele acertou a metade das questões, segue que:

[tex]\frac{13+0,25X}{20+X}=0,5[/tex]

[tex]13+0,25X=10+0,5X[/tex]

[tex]0,25X=3[/tex]

[tex]X=12[/tex]


A prova tem 20 + X itens, isto é, 32 itens.

Letra B.

---

14) Em cada um dos quadrados menores que formam o quadrado da Figura a seguir será colocado um dos números 1, 2 ou 3, de modo que não haja números repetidos na mesma linha nem números repetidos na mesma coluna.

A soma dos números representados pelas letras X e Y da Figura vale
(A) 4
(B) 5
(C) 6
(D) 2
(E) 3

A primeira fileira precisa ser preenchida com os números 2 e 3. O número 3 não pode ficar na primeira casa, pois já há um número 3 na primeira coluna.


Fica claro que falta apenas um número 1 para preencher a primeira coluna.


A primeira fileira precisa ser preenchida com os números 2 e 3. O número 3 não pode ficar na segunda casa, pois já há um número 3 na segunda coluna.
Isso nos leva a figura final:


Letra A.

---

15) Ao duplicar a largura de um determinado retângulo e reduzir à metade o comprimento desse mesmo retângulo, obtém-se um quadrado de perímetro P.
O perímetro do retângulo original é
(A) P
(B) 1,25P
(C) 2,5P
(D) 0,25 P
(E) 0,75P

Ao duplicar a largura do retângulo, essa ficou do mesmo tamanho que a metade do comprimento.
2L = 0,5C

O perímetro do quadrado resultante foi:
2L + 2L + 0,5C + 0,5C = P

Como 0,5C = 2L, segue que:
2L + 2L + 2L + 2L = P
8L = P

O perímetro original era igual a:
Perímetro = L + L + C + C
Perímetro = L + L + 4L + 4L
Perímetro = 10L

Como 8L = P, tem-se que 10L = (10/8)P.

Perímetro = (10/8)P
Perímetro = (5/4)P
Perímetro = 1,25P

Letra B.

---

Não encontrei nenhum caso passível de recurso.
Espero que as minhas resoluções tenham satisfeito às suas dúvidas, caso contrário deixe um comentário.
Se tiver alguma dúvida sobre a matéria, também pode perguntar. Tentarei responder o mais breve possível.

Prova 2016 - ESAF - Funai - Todos os Cargos - Raciocínio Lógico Comentada

prova FUNAI Raciocínio Lógico Comentada

http://www.esaf.fazenda.gov.br/assuntos/concursos_publicos/em-andamento-1/funai-2016/prova-objetiva-1_gabarito-1.pdf

---

21. Em uma cidade, 40% dos adultos são obesos, 45% dos adultos obesos são mulheres e 50% dos adultos não obesos são mulheres. Indique qual a probabilidade de que uma pessoa adulta da cidade escolhida ao acaso seja uma mulher.
A) 0,48
B) 0,49
C) 0,50
D) 0,51
E) 0,52

Se houvesse 100 pessoas na cidade, 40 delas seria obessas.
Entre essas 40 pessoas, 45% são mulheres.
45% de 40 é igual a 0,45*40 = 18 mulheres obesas.

Entre as 60 restantes, 50% são mulheres.
50% de 60 é igual a 30 mulheres.

Ao todo, há 48 mulheres nessa cidade. A probabilidade de escolher uma pessoa ao acaso e essa pessoa ser uma mulher é:
P(mulher) = número de mulheres / população total
P(mulher) = 48 / 100
P(mulher) = 0,48
Letra A.

---

22. Considerando os dados da questão anterior, indique qual a proporção de mulheres adultas que são obesas.
A) 5/8
B) 52%
C) 3/8
D) 11/26
E) 45%

Calculando que havia 18 mulheres obesas e 48 mulheres ao todo.
A proporção de mulheres adultas que são obesas é igual a 18/48, ou 3/8.
Letra C.

---

23. O triângulo I tem base b e altura h. O triângulo II tem base 25% maior e altura 20% menor que o triângulo I. A base do triângulo III é 1,25b e a altura é 0,8h.
Pode-se afirmar que:
A) A área do triângulo I é maior que a área do triângulo II.
B) A área do triângulo II é menor que a área do triângulo III.
c) Os triângulos II e III têm a mesma área que é maior que a área do triângulo I.
D) Os triângulos II e III têm a mesma área que é menor que a área de triângulo I.
E) Os três triângulos têm a mesma área.

A área de uma triângulo é igual a metade da multiplicação da base pela altura.

A área do triângulo I é igual a
[tex]\frac{bh}{2}[/tex].

A área do triângulo II é igual a
[tex]\frac{1,25b*0,8h}{2}[/tex]

[tex]=\frac{bh}{2}[/tex]


A área do triângulo II é igual a
[tex]\frac{0,8b*1,25h}{2}[/tex]

[tex]=\frac{bh}{2}[/tex]

Todas as áreas são iguais. A letra E responde a essa questão.

---

24. Considere as quatro letras A, C, G e T formando pares de letras nos quais A só forma par com T e C só forma par com G. Indique quantas sequências distintas de três pares ordenados de letras e com repetição podem ser formadas.
A) 4
B) 8
C) 16
D) 32
E) 64

Há dois pares (A,T) e (C,G).
Cada um dos pares pode ser permutados em duas ordens diferentes.
(A,T) e (T,A);
(C,G) e (G,C);

Digamos que há três casas que podem ser preechidas com qualquer um dos quatro pares.
_ * _ * _

Pelo princípio fundamental da contagem, a primeira casa pode ser preenchida com 4 pares quaisquer:
4 * _ * _

A segunda e terceira casa também.
4 * 4 * 4
Totalizando 64 sequências distintass.
Letra E.

---

25. O limite da série infinita S de razão 1/3,
S = 9 + 3 + 1 + 1/3 + 1/9 + ... é:
A) 13,444....
B) 13,5
C) 13,666....
D) 13,8
E) 14

Basta multiplicar a sequência pela razão e em seguida subtrair o resultado da sequência. Vai ficar apenas o primeiro termo do lado direito da equação e do lado esquerdo vai ficar (1-razão) multiplicado por S:
S = 9 + 3 + 1 + 1/3 + 1/9 + ...
(1/3)S = 3 + 1 + 1/3 + 1/9 + 1/27...

S - (1/3)S = 9
(2/3)S = 9
S = (3/2)9
S = 27/2
S = 13,5

Letra B

---

26. Sejam as proposições p e q onde p implica logicamente q e sejam as negações ~p e ~q. Tem-se que:
A) p é equivalente logicamente a q.
B) p implica logicamente q e q implica p.
C) p implica logicamente q e ~p implica ~q.
D) p e ~q é uma contradição.
E) p ou ~q é uma tautologia.

Se P e Q são proposições distintas, segue que P não é equivalente logicamente a Q.
P implica Q, conforme diz o enunciado. Concluir a partir dessa informação que Q implica P é uma falácia conhecida por afirmação do consequente.
Concluir que ~P implica ~Q é outra falácia conhecida como negação do antecedente.
P e ~Q é uma contradição, pois P implica Q. Logo, se P ocorreu, então Q também ocorreu. Um caso em que P ocorreu e Q não ocorreu contradiz o enunciado.
P ou ~Q não é uma tautologia, porque os valores lógicos de P e Q podem ser respectivamente falso e verdadeiro. Não haveria conflito com o enunciado esse caso em que P não ocorreu, mas Q ocorreu. Haveria apenas conflito com a letra E.
Gabarito: D.

---

27. Sejam as proposições p e q onde p implica logicamente q. Diz-se de maneira equivalente que:
A) p é condição suficiente para q.
B) q é condição suficiente para p.
C) p é condição necessária para q.
D) p é condição necessária e suficiente para q.
E) q não é condição necessária para p.

Quando uma proposição P implica uma proposição Q, diz-se que P é condição suficiente para Q porque é suficiente P ocorrer para que Q ocorra.
Por exemplo, "se choveu, então o pátio está molhado". Chover é condição suficiente para o pátio estar molhado, pois basta ter chovido para molhar o pátio.
Diz-se que Q é condição necessária para P, porque se P ocorreu é necessário que Q tenha ocorrido também. Entende-se por aí que se Q não ocorreu, P também não ocorreu por contraposição.
Letra A.

---

28. Seja NE a abreviatura de Nordeste. A negação de “O Piauí faz parte do NE ou o Paraná não faz parte do NE” é:
A) o Piauí não faz parte do NE.
B) o Paraná faz parte do NE.
C) o Piauí não faz parte do NE ou o Paraná faz parte do NE.
D) o Piauí não faz parte do NE e o Paraná faz parte do NE.
E) o Piauí e o Paraná fazem parte do NE.

Para negar uma proposição composta unida por uma disjunção inclusiva (ou) é necessário que ambas proposições simples sejam falsas.
Ou seja, "o Piauí não faz parte do NE" E "o Paraná faz parte do NE". Conforme consta na Letra D.

---

29. Seja a proposição: “Se um elemento possui a propriedade P então ele possui também a propriedade Q”. Para demonstrar que esta proposição é falsa, basta mostrar que:
A) todo elemento que possui a propriedade Q também possui a propriedade P.
B) existe um elemento que não possui nem a propriedade P nem a propriedade Q.
C) existe um elemento que possui a propriedade P, mas não possui a propriedade Q.
D) existe um elemento que não possui a propriedade P.
E) existe um elemento que possui a propriedade Q, mas não possui a propriedade P.

O enunciado está afirmando que todo elemento que possui a propriedade P possui também a propriedade Q.
Para contrariar basta encontrar um elemento que possui P, mas não possui Q.
Letra E.

---

30. Sejam as proposições (p) e (q) onde (p) é V e (q) é F, sendo V e F as abreviaturas de verdadeiro e falso, respectivamente. Então com relação às proposições compostas, a resposta correta é:
A) (p) e (q) são V.
B) Se (p) então (q) é F.
C) (p) ou (q) é F.
D) (p) se e somente se (q) é V.
E) Se (q) então (p) é F.

Tabela verdade para finalizar:

Letra B.

010.01 - Análise Combinatória - Exercícios Comentados

1) (2010 - Cespe) Em uma sala de aula foram escolhidos 5 alunos para se formar uma comissão de 2 elementos. Acerca dessa comissão, julgue o item que se segue.

Se um dos membros da comissão tiver a missão de dialogar com a direção da escola e o outro, com a secretária da escola, então o número máximo de comissões distintas que podem ser formadas é igual a 18.

Como os papéis da comissão são relevantes, a ordem dos elementos importa.
Isso é as comissões {João, Maria} e {Maria, João} são distintas a depender de qual dos dois alunos irá dialogar com a direção.
Como a ordem importa, deve se usar a fórmula de Arranjo simples.

[tex]A_{s}(m,p)=\frac{m!}{(m-p)!}[/tex] em que m é a quantidade de alunos e p é a quantidade de elementos para compor a comissão.

[tex]A_{s}(5,2)=\frac{5!}{(5-2)!}[/tex]

[tex]A_{s}(5,2)=\frac{5!}{3!}[/tex]

[tex]A_{s}(5,2)=\frac{5*4*3*2*1}{3*2*1}[/tex]

[tex]A_{s}(5,2)=5*4[/tex]

[tex]A_{s}(5,2)=20[/tex]

O número máximo de comissões distintas que podem ser formadas é superior a 18.

---

2) (2013 - ESAF) O número de anagramas da palavra FAZENDA que começam com FA e nessa ordem é igual a:
A) 130
B) 124
C) 120
D) 115
E) 136

Anagramas são permutações entre uma sequência de letras.
Se o anagrama deve necessariamente começar com FA, então é uma permutação entre as 5 letras restantes.
F A _ _ _ _ _
Você pode pensar que a primeira casa vazia pode ser preenchida por qualquer uma das 5 letras {Z, E, N, D, A}.
A segunda casa pode ser preenchida por qualquer uma das 4 letras restante.
A terceira casa pode ser preenchuda por 3 letras, a segunda por duas e a última letra irá ficar na casa restante.

Trata-se de uma permutação simples de 5 elementos.
P(5) = 5!
P(5) = 5 * 4 * 3 * 2 * 1
P(5) = 120

---

3) (2010 - Cespe) Para a codificação de processos, o protocolo utiliza um sistema com cinco símbolos, sendo duas letras de um alfabeto com 26 letras e três algarismos, escolhidos entre os de 0 a 9. Supondo que as letras ocupem sempre as duas primeiras posições, julgue o item que se segue.

O número de processos que podem ser codificados por esse sistema utilizando-se letras iguais nas duas primeiras posições do código é superior a 28.000.

O código tem o formato LLAAA, em que L é uma das 26 letras do alfabeto e A é um algarismo de 0 a 9.
As duas primeiras letras serão idênticas, logo há 26 alternativas para prencher as duas primeiras casas.
26 * 1 * A * A * A

O enunciado não informa se os algarismos devem ser distintos, portanto é válido assumir que possam ser todos iguais. Como há 10 dígitos de 0 a 9, então há 10 alternativas distintas para cada uma das casas dos algarismos.
26 * 1 * 10 * 10 * 10

Ao todo há 26.000 processos que podem ser codificados por esse sistema utilizando-se letras iguais nas duas primeiras posições, um número inferior a 28.000.

---

4) (2014 - Cespe) Sabendo-se que uma repartição possui 30 servidores, sendo 10 do sexo feminino, julgue o item abaixo.
A quantidade de maneiras distintas de se selecionar 5 servidores dessa repartição de forma que 4 sejam do sexo feminino é inferior a 4.000.

Será formado um grupo de 1 homem e 4 mulheres. A ordem dos integrantes não importa, então deve-se usar a fórmula da combinação.
Há C(20,1) maneiras distintas de se escolher 1 homem entre 20.
Há C(10,4) maneiras distintas de se escolher 4 mulheres entre 10.
[tex]C(m,p)=\frac{m!}{p!(m-p)!}[/tex] em que m é a quantidade de alunos e p é a quantidade de elementos para compor a comissão.

[tex]C(20,1)=\frac{20!}{1!(20-1)!}[/tex]

[tex]C(20,1)=\frac{20!}{1!*19!}[/tex]

[tex]C(20,1)=20[/tex]


[tex]C(10,4)=\frac{10!}{4!(10-4)!}[/tex]

[tex]C(10,4)=\frac{10!}{4!*6!}[/tex]

[tex]C(10,4)=\frac{10*9*8*7}{4*3*2*1}[/tex]

[tex]C(10,4)=10*3*7[/tex]

[tex]C(10,4)=210[/tex]

A quantidade de maneiras distintas de se selecionar 5 servidores dessa repartição, sendo 1 homem E 4 mulheres é
= C(20,1) * C(10,4)
= 20 * 210
= 4.200

Uma quantidade superior a 4.000.

---

5) (2013 - FGV) O número de maneiras diferentes de se colocar as letras da sigla CONDER em fila, de modo que a fila comece por uma vogal, é
A) 240.
B) 120.
C) 96.
D) 72.
E) 60.

Pode se pensar que há 6 casas a serem preenchidas com as letras {C, O, N, D, E, R}.
_ * _ * _ * _ * _ * _

Na primeira casa deve ter uma vogal, logo há duas opções para a primeira casa, a letra "O" ou a letra "E".
2 * _ * _ * _ * _ * _

As demais letras podem ser permutadas entre as 5 casas restantes.
2 * 5 * 4 * 3 * 2 * 1

Ao todo, há 2* P(5) = 2 * 120 = 240 maneiras distintas de colocar as letras da sigla em fila começando por uma vogal.

---

6) (2013 - CESGRANRIO) Cinco pessoas devem ficar em fila, sendo que duas delas (João e Maria) precisam ficar sempre juntas.
De quantas formas diferentes essas pessoas podem-se enfileirar?
A) 48
B) 50
C) 52
D) 54
E) 56

Como João e Maria devem estar juntos, imagine-os como um bloco, {A, B}.
O par {A, B} pode ser permutados de 2 formas distintas: (A, B) e (B, A).

Na fila, há outras 3 pessoas {C, D, E}.
Em conjunto com o bloco {A, B}, há 4 elementos na fila. Então a quantidade de formas diferentes que essas pessoas podem se enfileirar é uma permutação de 4 elementos E uma permutação do bloco.
P(4) * P(2) = (4 * 3 * 2 * 1) * (2 * 1) = 48 maneiras distintas.

---

7) (2015 - FGV) Em uma urna há somente bolas brancas, bolas pretas e bolas vermelhas. Para cada bola branca há três bolas pretas e para cada duas bolas pretas há cinco bolas vermelhas.

A razão entre a quantidade de bolas pretas e a quantidade total de bolas na urna é:
A) 3/10
B) 4/19
C) 5/21
D) 6/23
E) 7/25

B = Bolas Brancas
P = Bolas pretas
V = Bolas vermelhas

Para cada bola branca há três bolas pretas. Se houvesse 10 bolas brancas (B=10), então haveria 30 bolas pretas (P=30).
Como P é maior que B, é necessário multiplicar B por três para manter a igualdade da equação.
3B = P
B = [tex]\frac{1}{3}[/tex]P

Para cada duas bolas pretas há cinco bolas vermelhas.
P = [tex]\frac{2}{5}[/tex]V
V = [tex]\frac{5}{2}[/tex]P

A razão, R, entre a quantidade de bolas pretas e a quantidade total de bolas na urna é

[tex]R=\frac{P}{P+B+V}[/tex]

[tex]R=\frac{P}{P+\frac{1}{3}P+\frac{5}{2}P}[/tex]

[tex]R=\frac{P}{P+\frac{2}{6}P+\frac{15}{6}P}[/tex]

[tex]R=\frac{P}{P+\frac{17}{6}P}[/tex]

[tex]R=\frac{P}{\frac{23}{6}P}[/tex]

[tex]R=\frac{6}{23}[/tex]

---

8) (2016 - MSCONCURSOS) Dona Amélia comprou 5 ovos de páscoa para compor a cesta de páscoa da família. Considerando que ela teve 9 opções de sabores para escolher, é correto afirmar que o número de maneiras possíveis para Dona Olga ter comprado esses ovos de páscoa é igual a
A) 126.
B) 495.
C) 715.
D) 1287.
A ordem em que os ovos são colocados na cesta não importa, então trata-se de uma combinação com repetição de 5 entre 9 elementos.

[tex]C_{rep}(m,p) = C(m+p-1,p)[/tex]

[tex]C_{rep}(9,5) = C(13,5)[/tex]

[tex]C(13,5)=\frac{13!}{5!(13-5)!}[/tex]

[tex]C(13,5)=\frac{13!}{5!8!}[/tex]

[tex]C(13,5)=\frac{13*12*11*10*9}{5*4*3*2}[/tex]

[tex]C(13,5)=13*3*11*3[/tex]

[tex]C(13,5)=1287[/tex]

Explicação sobre a fórmula

Se não ficou claro para você o motivo por que [tex]C_{rep}(m,p) = C(m+p-1,p)[/tex], segue uma analogia.
Imagine que há 9 caixas com ovos de páscoa, cada caixa com um sabor diferente.
As caixas estão alinhadas e divididas por 8 divisórias. Na imagem as divisórias estão em vermelho:


Uma possível combinação de 5 ovos poderia ser presentada pela imagem:

É importante notar que qualquer combinação depende somente onde os ovos estão localizados com relação às divisórias.
Se essa combinação for representada por x e D em que "x" é um ovo e "D" uma divisória, ficaria assim:
{x,x,x,D,D,x,D,x,D,D,D,D,D}

Uma segunda combinação

Seria {D,D,D,x,D,x,D,x,D,x,x,D,D}.

De quantas formas você pode alocar os cinco ovos entre as 9 caixas? Como o que importa é apenas a ordem dos ovos e das divisórias. Segue que é uma permutação de 13 elementos, com 5 "x" repetidos e 8 "D" repetidos.
[tex]P_{rep}(13)=\frac{13!}{5!8!}=C(13,5)[/tex]

---

9) (2015 - FGV) No primeiro turno do campeonato piauiense de futebol 6 times participam, mas somente 4 chegam às semifinais.
O número de possibilidades diferentes para o conjunto dos 4 times que estarão nas semifinais é:
A) 10;
B) 12;
C) 15;
D) 18;
E) 30.

As chaves (ordem) não importam, então trata-se de uma combinação de 4 elementos entre 6. [tex]C(6,4)=\frac{6!}{4!(6-4)!}[/tex]

[tex]C(6,4)=\frac{6!}{4!2!}[/tex]

[tex]C(6,4)=\frac{6*5}{2}[/tex]

[tex]C(6,4)=3*5[/tex]

[tex]C(6,4)=15[/tex]

---

10) (2010 - Cespe) Em uma sala de aula foram escolhidos 5 alunos para se formar uma comissão de 2 elementos. Acerca dessa comissão, julgue o item que se segue.
Se os alunos da comissão tiverem funções idênticas, então a quantidade máxima de comissões distintas que podem ser formadas é igual a 10.

Como as funções são idênticas, não importa a ordem dos alunos dentro da comissão. Isto é, o conjunto {João, Maria} é igual ao conjunto {Maria, João}. Como a ordem não importa, deve-se usar a fórmula da combinação de 2 elementos entre 5. [tex]C(5,2)=\frac{5!}{2!(5-2)!}[/tex]

[tex]C(5,2)=\frac{5!}{2!3!}[/tex]

[tex]C(5,2)=\frac{5*4}{2}[/tex]

[tex]C(5,2)=5*2[/tex]

[tex]C(5,2)=10[/tex]

Correta a questão.

---

11) (2015 - FGV) Sete pessoas formam uma fila e duas delas serão escolhidas para receber um brinde. O número de maneiras diferentes de escolher duas pessoas da fila que não sejam vizinhas é;
A) 15;
B) 18;
C) 20;
D) 24;
E) 30.

A quantidade de maneiras diferentes de se escolher 2 pessoas entre 7 pode ser calculada por meio da fórmula da combinação, pois a ordem das pessoas não importa. [tex]C(7,2)=\frac{7!}{2!(7-2)!}[/tex]

[tex]C(7,2)=\frac{7!}{2!5!}[/tex]

[tex]C(7,2)=\frac{7*6}{2}[/tex]

[tex]C(7,2)=7*3[/tex]

[tex]C(7,2)=21[/tex]

O enunciado proíbe que as duas pessoas selecionadas sejam vizinhas. Como há 7 pessoas na fila, há 6 pares de vizinhos. Você pode pensar que as pessoas estão de mãos dadas e contar quantas mão estão unidas. Se tivesse duas pessoas, seriam 2 mãos. Se tivesse três pessoas na fila, seriam 2 mãos. O número de mãos é inferior em uma unidade ao número de pessoas na fila.

Há 21 pares diferentes ao todo.
Há 6 pares vizinhos.
Então, há 15 pares que cumprem a condição do enunciado.

---

12) (2012 - CESGRANRIO) No estojo de Pedro, há nove canetas idênticas, exceto pelas cores: três são azuis, quatro são vermelhas e duas são pretas. O professor de matemática de Pedro o desafiou perguntando-lhe qual é o menor número de canetas que ele deve retirar, aleatoriamente, de seu estojo para garantir que, dentre as canetas retiradas, haja, pelo menos, uma caneta de cada cor
Que número é esse?

A) 3
B) 6
C) 7
D) 8
E) 9

Para responder à questão, deve-se considerar a pior hipótese possível, ou seja, a hipótese em que Pedro retira o maior número possível de canetas da mesma cor.
Para garantir que ele tenha pelo menos uma caneta de cada cor, Pedro deve retirar 8 canetas.
Se ele retirar 7 canetas aleatoriamente, ele pode ter o azar de retirar as quatro canetas vermelhas e as três canetas azuis. Nessa pior cenário possível, Pedro não tem uma caneta de cada cor, porque não tem canetas pretas. A próxima retirada vai garantir que tenha uma preta. Por isso, a resposta é a letra D.

---

13) (2014 - UFBA) O centro de uma cidade é uma região plana, cortada por 5 ruas no sentido leste-oeste e 7 ruas no sentido norte-sul, como na ilustração, na qual o tracejado representa um trecho em obras fechado para o tráfego. Se um táxi parte da extremidade noroeste dessa região, seguindo essas ruas, sempre nos sentidos leste ou sul, há exatamente 140 caminhos distintos que ele pode usar para chegar à extremidade sudeste.


Há 5 ruas horizontais e 7 ruas verticais.

Para chegar do noroeste ao sudeste são necessários 10 passos, 4 na direção Sul e 6 na direção Leste em qualquer ordem. Se os passos puderem ser representados pela sequência (S, S, S, S, L, L, L, L, L, L), então fica claro que a resposta, sem levar em contar a restrição, seria uma permutação com repetição entre esses 12 elementos.

Exemplo de percursos que atendem ao trajeto:
(S, L, L, S, S, L, L, S, L, L)
(L, S, S, L, L, L, S, L, L, S)

Como há duas ruas bloqueadas. Todas as sequências que começam por (L, L, ...) não são válidas.

É necessário calcular dois grupos de permutação com repetição.
1) Os que começam por um passo ao Sul, pois a partir de então não há como voltar às ruas bloqueadas, visto que o táxi só viaja nas direções sul ou leste.
2) Os que começam por m passo ao Leste seguindo por um passo ao Sul.

Isto é:
1) (S, ... ) Sobram 9 elementos, sendo três letras S e seis letras L.
2) (L, S, ...) Sobram 8 elementos, sendo três letras S e cinco letras L.

As fórmulas são respectivamente:
1) [tex]\frac{P(9)}{P(3)*P(6)}=\frac{9!}{3!*6!}=84[/tex] rotas começando pelo Sul.

2) [tex]\frac{P(8)}{P(3)*P(5)}=\frac{8!}{3!*5!}=56[/tex] rotas começando pelo Leste e seguindo ao Sul.


Ao todo 84 + 56 = 140.

Nesse vídeo há uma forma alternativa de calcular o número de rotas.
https://youtu.be/9QduzzW10uA
Tem legenda em português.

---

002.01 Conectivos Lógicos - Exercícios

1) (2016 - Cespe) Considere as seguintes proposições para responder a questão.
P1: Se há investigação ou o suspeito é flagrado cometendo delito, então há punição de criminosos.
P2: Se há punição de criminosos, os níveis de violência não tendem a aumentar.
P3: Se os níveis de violência não tendem a aumentar, a população não faz justiça com as próprias mãos.
A quantidade de linhas da tabela verdade associada à proposição P1 é igual a
A) 32.
B) 2.
C) 4.
D) 8.
E) 16.

A tabela verdade lista todas as associações de valores lógicos que cada uma das proposições pode assumir.
No caso de duas proposições por exemplo, existem quatro casos possíveis:
1)A primeira proposição é verdadeira e a segunda é veradeira;
2)A primeira proposição é verdadeira e a segunda é falsa;
3)A primeira proposição é falsa e a segunda é veradeira;
4)A primeira proposição é falsa e a segunda é falsa;
A introdução de uma nova proposição faz com que o número de linhas (excluíndo o cabeçalho) da tabela duplique.
A relação matemática entre o número de proposições X e número de linhas Y se dá por:
[tex]Y=2^{x}[/tex]

A proposição P1 do enunciado é composta por três proposições simples:
P - Há investigação;
Q - O suspeito é flagrado comentendo delito;
R - Há punição de criminosos.

Como há três proposições simples, então basta substituir X por 3 na fórmula anterior para calcular o número de linhas da tabela verdade.
[tex]Y=2^{x}[/tex]
[tex]Y=2^{3}[/tex]
[tex]Y=8[/tex]

Exemplo de tabelas verdade. Veja como o número de linhas vai duplicando na medida que são introduzidas novas proposições simples.

---

2) (2016 - Cespe) Com relação a lógica proposicional, julgue o item subsequente.

Na lógica proposicional, a oração “Antônio fuma 10 cigarros por dia, logo a probabilidade de ele sofrer um infarto é três vezes maior que a de Pedro, que é não fumante” representa uma proposição composta.

Uma proposição simples é uma sentença declarativa que pode ser avaliada ora como verdadeira, ora como falsa.
Uma proposição composta é a reunião de duas ou mais proposições simples unidas por conectivos lógicos.
O ideal é o candidato conseguir identificar as proposições simples que compõem o enunciado.

P = "Antônio fuma 10 cigarros por dia"
P é uma sentença declarativa que pode ser julgada como verdadeira ou falsa.

Q = "A probabilidade de Antônio sofrer um infarto é três vezes maior que a de Pedro"
Q é outra sentença declarativa.

R = "Pedro é não fumante"
É a terceira proposição simples.

Basta isso para responder a questão como certa.

Professor, como traduzir o enunciado para a simbologia lógica? Quais são os conectivos usados?
Na hora de traduzir, eu sempre buscar captar o significado e implicações da frase. Eu traduziria a frase do enunciado para a simbologia lógica da seguinte maneira:

(P^R)→Q

Leia-se "SE Antônio fuma 10 cigarros por dia E Pedro é não fumante, ENTÂO a probabilidade de Antônio sofrer um infarto é três vezes maior que a de Pedro".

---

3) Julgue o item a seguir, relativos a raciocínio lógico e operações com conjuntos.
A sentença “Bruna, acesse a Internet e verifique a data da aposentadoria do Sr. Carlos!” é uma proposição composta que pode ser escrita na forma p ∧ q.

Uma proposição simples é uma sentença declarativa que pode ser avaliada como verdadeira ou como falsa.
Não é possível atribuir um valor lógico para frases no imperativo tais como "Bruna, acesse a interenet!" ou ainda "Bruna, verifique a data da aposentadoria do Sr. Carlos!". Portanto, a sentença do enunciado não é uma proposição.
Também não são proposição
Frases interrogativas: "Que ganhou o jogo?"
Frases opinativas: "Eu considero que Getúlio Vargas como um bom presidente."
Frases exclamativas: "Opa, cuidado!"
Sentenças abertas: "x = tudo" (é necessário definir o que é x para poder avaliar a sentença)

---

4) (2016 - FCC) Um exame é constituído de cinco perguntas, sendo que cada uma deve ser respondida com verdadeiro (V) ou falso (F). A tabela abaixo mostra as respostas assinaladas por quatro alunos.

Sabendo-se que um dos quatro alunos acertou todas as respostas, outro acertou somente duas das respostas, e outro errou todas as respostas, o número de respostas certas do aluno restante foi
A) 3.
B) 4.
C) 1.
D) 2.
E) 5.

O primeiro passo aqui é reconhecer que o caderno de resposta de dois alunos não terá nenhuma resposta igual, porque um dos alunos acertou todas as questões e outro errou todas as questões.
Analisando os cadernos de resposta observa-se que João e Pedro não concordoram em nenhuma questão. Logo, um deles gabaritou e o outro tirou zero.

O segundo passo é testar ambas as hipóteses. Se João tivesse gabaritado o caderno, então ambos Luís e Mário teriam acertado 3 questões.

Essa hipótese contrdiz o enunciado que nos informa que um dos colegas acertou exatamente duas questões. Logo, discarta-se a hipótese de que João tenha gabaritado a prova.

Caso Pedro tenha gabaritado a prova, segue que Luís e Mário acertaram exatamente duas questões.

---

5) (2013 - FGV) Um contra‐exemplo para uma determinada afirmativa é um exemplo que a contradiz, isto é, um exemplo que torna a afirmativa falsa.
No caso de afirmativas do tipo “SE antecedente ENTÃO consequente", um contra‐exemplo torna o antecedente verdadeiro e o consequente falso.
Um contra‐exemplo para a afirmativa “SE x é múltiplo de 7
ENTÃO x é um número ímpar" é:
A) x = 7
B) x = 8
C) x = 11
D) x = 14
E) x = 21

Temos que "x é múltiplo de 7" é o antecedente e "x é um número ímpar" é o consequente.
Um contra-exemplo para a afirmativa torna o antecedente verdadeiro E o consequente falso. Isto é, "x é múltiplo de 7" E "x NÃO é um número ímpar".
Basta encontrar um múltiplo de 7 par nas alternativas, sejam 0, 14, 28, 42, 56, 70, 84, ....
A letra D responde à questão.

---

6) (2011 - CESPE) Entende-se por proposição todo conjunto de palavras ou símbolos que exprimem um pensamento de sentido completo, isto é, que afirmam fatos ou exprimam juízos a respeito de determinados entes. Na lógica bivalente, esse juízo, que é conhecido como valor lógico da proposição, pode ser verdadeiro (V) ou falso (F), sendo objeto de estudo desse ramo da lógica apenas as proposições que atendam ao princípio da não contradição, em que uma proposição não pode ser simultaneamente verdadeira e falsa; e ao princípio do terceiro excluído, em que os únicos valores lógicos possíveis para uma proposição são verdadeiro e falso. Com base nessas informações, julgue os itens a seguir.

Segundo os princípios da não contradição e do terceiro excluído, a uma proposição pode ser atribuído um e somente um valor lógico.
O princípio da não contradição diz que nenhuma proposição pode ser verdadeira E falsa ao mesmo tempo.

O princípio do terceiro excluído complementa a ideia anterior e define que a proposição ora assume valor verdadeiro, ora assume valor falso, excluindo quaisquer outras possibilidades.

Portanto, apenas um valor lógico (ora verdadeiro, ora falso) pode ser atribuído a uma proposição.

---

7) (2013 - IBFC) Sejam as afirmações:

I. Se o valor lógico de uma proposição p é falso e o valor lógico de uma proposição q é verdadeiro, então o valor lógico da conjunção entre p e q é verdadeiro.
II. Se todo X é Y, então todo Y é X.
III. Se uma proposição p implica numa proposição q, então a proposição q implica na proposição p.

Pode-se afirmar que são verdadeiras:
a) Todas
b) Somente duas delas
c) Somente uma delas
d) Nenhuma

I. É falsa, a conjunção só é verdadeira quando ambas as proposições são verdadeiras. Como o valor lógico de p é falso, segue que (p ^ q) é falso.
II. É falsa. "Todo X é Y" equivale a construção da condicional "Se é X, então é Y". A partir dessa informação, não se pode afirmar que "Se é Y, então é X", pois é uma conclusão falaciosa conhecida como afirmação do consequente.
III. É falsa. Novamente, uma falácia de afirmação do consequente.
Nenhuma das afirmações é verdadeira.

---

8) (2012 - IF-CE) Considere os conectivos * e # com a seguinte interpretação:

p * q é verdadeira, somente quando p e q têm o mesmo valor lógico.
p # q é falsa, somente quando p é falsa e q é verdadeira.

Nessas condições, dentre todas as escolhas de valor lógico para as proposições simples A, B e C, a fórmula A # (B * C) é falsa

A) nenhuma vez.
B) duas vezes.
C) três vezes.
D) cinco vezes.
E) todas as vezes.

Para A # (B * C) ser falso é necessário que:
A seja falso
(B * C) seja verdadeiro

Para (B * C) ser verdadeiro é necessário que B e C tenho o mesmo valor lógico. Ou seja, há dois casos.
(B, C) = (V, V)
(B, C) = (F, F)

Logo, só há dois casos em que A # (B * C) é verdadeiro:
(A, B, C) = (F, V, V)
(A, B, C) = (F, F, F)


Relembrando as regras do enunciado, é possível resolver por meio da tabela verdade.
B*C é verdadeira, somente quando B e C têm o mesmo valor lógico (letras azuis).
A#(B¨*C) é falsa, somente quando A é falsa e (B*C) é verdadeira (fundo verde claro).

Tabela Verdade:

A	B	C	B*C	A#(B*C)
V	V	V	V	V
V	V	F	F	V
V	F	V	F	V
V	F	F	V	V
F	V	V	V	F
F	V	F	F	V
F	F	V	F	V
F	F	F	V	F

20 questões comentadas avulsas 06 (para organizar mais tarde)

Completarei 30 em breve. Mais virão.
...
6) 7) (2016 - FUNRIO)Realizou-se uma pesquisa com 200 hipertensos para identificar a ocorrência dos seguintes fatores de risco dessa doença: sedentarismo, obesidade e histórico familiar. Desses hipertensos, cinquenta são obesos, setenta são sedentários, oitenta possuem histórico de doença na família e cinquenta não apresentam nenhum desses três fatores de risco. Assim sendo, a maior quantidade de hipertensos desse grupo que possui exatamente dois desses fatores de risco é:
A) 20.
B) 25.
C) 30.
D) 40.
E) 50.

---

8) (2016 - FUNRIO) A seguinte Tabela apresenta resultados de uma pesquisa sobre a quantidade de filhos de 600 casais de uma determinada cidade.

Número de Filhos	Quantidade de Famílias
0	300
1	200
2	50
3	X
4	Y

Sabendo-se que a quantidade média de filhos por casal da pesquisa é 0,76, a quantidade de casais da pesquisa que possuem 4 filhos é
A) 3.
B) 6.
C) 10.
D) 12.
E) 15.

O enunciado diz que 600 famílias foram pesquisadas.
300+200+50+X+Y = 600
X + Y + 550 = 600
X + Y = 50

A quantidade total de filhos = (0*300) + (1*200) + (2*50) + (3*X) + (4*Y)
A quantidade total de filhos = 0 + 200 + 100 + 3X + 4Y
A quantidade total de filhos = 300 + 3X + 4Y

A média de filhos por família é 0,76.
Média = número de filhos / número de famílias
0,76 = (300 + 3X + 4Y) / 600
456 = 300 + 3X + 4Y
3X + 4Y = 156

Ficamos com um sistema de equações:
[tex]\left\{\begin{matrix} 3X+4Y=156\\X+Y=50 \end{matrix}\right.[/tex]

Multiplica a primeira equação por 3.
[tex]\left\{\begin{matrix} 3X+4Y=156 & \\ 3X+3Y=150 & \text{mulplicada por 3} \end{matrix}\right.[/tex]

Subtrai a primeira equação pela segunda para obter Y = 6.

---

9)(2016 - MSCONCURSOS) O número de subconjuntos próprios de A = {x ∈ Z ; 12 < x < 17} é:
A) 14
B) 16
C) 32
D) 64
B é um subconjunto próprio de A se B ⊆ A (leia-se o conjunto B está contido no conjunto A) e se B≠A. Alguns livros usam a anotação B ⊂ A.
O conjunto A = {13, 14, 15, 16} possui 4 elementos.
Como há 4 elementos, há [tex]2^{4}[/tex] subconjuntos (impróprios). Os subconjuntos de A são:
{{∅}, {13}, {14}, {15}, {16}, {13, 14}, {13, 15}, {13, 16}, {14, 15}, {14, 16}, {15, 16}, {13, 14, 15}, {13, 14, 16}, {13, 15, 16}, {14, 15, 16}, {13, 14, 15, 16^}}
Os subconjuntos {13, 14, 15, 16} é igual a A e portanto não é um subconjunto próprio.
O examinador considerou que {∅} também não é um subconjunto próprio de A, mas isso é debatível.
A letra A é que melhor responde à questão.

---

10) (2015 - COPEVE-UFAL) Se a numeração dos imóveis das ruas somente admitisse números primos, obedecendo rigorosamente a ordem crescente dos números e sem pular nenhum número,
A) em todas as ruas com mais de 6 casas, haveria o imóvel de número 41.
B) em ruas com mais de 500 casas, haveria um imóvel de número 143.
C) em avenidas com mais de 100 imóveis, haveria imóveis de números 43, 83 e 101.
D) e se todas as ruas possuem pelo menos um imóvel, haveria sempre um imóvel de número 1, pois 1 é primo.
E) assim como hoje, existiriam imóveis numerados com números ímpares e números pares, na mesma proporção.

A) Uma rua com 7 casas é uma rua com mais de 6 casas. Os sete primeiros números primos são 2, 3, 5, 7, 11, 13, e 17.
Portanto. é possível existir uma rua com mais de 6 casa em que não haveria imóvel de número 41.

B) O número 143 é composto (não é primo). 143 = 11 * 13.

C) Certo. Todos os 3 números apresentados são primos. Não precisa saber qual é o centésimo número primo, basta notar que 101 é bem aquém de ser o centésimo. É o 26º número primo.

D) O número 1 não é primo.

E) O único número primo par é o 2. A menos que a rua conte com apenas dois imóveis, a proporção favoreceria os números ímpares.

---

11) (2016 - MsConcursos) Observe o diagrama lógico seguinte, formado por duas camadas de células retangulares, sequenciais, cujos valores internos são constituídos seguindo determinado padrão lógico.

O valor de x no diagrama acima é:
A) 345
B) 343
C) 339
D) 337

A sequência de cima é formada por um acréscimo de 2 a cada termo. Vou chamá-la de A.
A sequência de baixo é formada por um acréscimo de 4 a cada termo. Vou chamá-la de B.

Os termos sequências podem ser descritos pela seguinte regra em que n é a posição do termo da sequência.
[tex]A_{n}=2n-1[/tex]
[tex]B_{n}=4n-1[/tex]

Assim temos
[tex]A_{1}=2(1)-1=2-1=1[/tex]
[tex]A_{2}=2(2)-1=4-1=3[/tex]
[tex]A_{3}=2(3)-1=6-1=5[/tex]
[tex]A_{4}=2(4)-1=8-1=7[/tex]
...
e
[tex]B_{1}=4(1)-1=4-1=3[/tex]
[tex]B_{2}=4(2)-1=8-1=7[/tex]
[tex]B_{3}=4(3)-1=12-1=11[/tex]
[tex]B_{4}=4(4)-1=16-1=15[/tex]
...

A posição do termo 171 na sequência A é
[tex]A_{n}=2n-1[/tex]
[tex]171=2n-1[/tex]
[tex]172=2n[/tex]
[tex]n=86[/tex]º termo

O 86º termo na sequência B será
[tex]B_{n}=4n-1[/tex]
[tex]B_{86}=4(86)-1[/tex]
[tex]B_{86}=344-1[/tex]
[tex]B_{86}=343[/tex]

---

12) Um dado é lançado 6 vezes. É correto afirmar que a probabilidade de ocorrer exatamente um par de 3, ou exatamente um par 4 ou ainda exatamente um 3 e um 4 é 80/243.

A questão considerou válida quaisquer combinações que contivessem exatamente um par de "3", ou exatamente um par de "4" ou ainda um "3" e um "4".
Exemplo de combinações válidas:
{3, 5, 1, 2, 3, 6}
{1, 1, 5, 4, 4, 2}
{2, 5, 6, 3, 5, 4}

Então a probabilidade de sair o 3 ou o 4 em um determinado lançamento é 1/3. Vou chamar essa probabilidade de P(A) = 1/3.
A probabilidade de sair qualquer outro número é igual a 2/3. Vou chamar essa probabilidade de P(N) = 2/3.
Como ele mediu a probabilidade de sair exatamente um par de "3" ou "4" ou 1 de ambos, então ele calculou a probabilidade de sair o conjunto:
{A, A, N, N, N, N}
A probabilidade de sair A e A é igual a P(A) * P(A) = (1/3)2 = 1/9
A probabilidade de sair N e N e N e N é igual a P(N)4 = (2/3)4 = 16/81

Agora observe que o par de A pode aparecer em diversas posições, tais como:
{A, N, A, N, N, N}
{N, N, A, N, A, N}
{N, N, N, A, N, A} etc.
Ou seja, há 6 posições em que os 2 A podem estar. Isso é calculável por meio da fórmula das combinações C(6,2) = 6! / 4!2! = 15

Ao todo temos:
P(total) = C(6,2) * P(A)2 * P(N)4
P(total) = 10 * 1/9 * 16/81
P(total) = 240 / 729
P(total) = 80 / 243
Certa a questão.

---

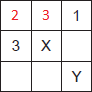
13)(2013 - CESGRANRIO) Se os algarismos de 1 a 9 forem colocados, sem repetição, nos quadrados da Figura a seguir, de modo que a soma dos algarismos dispostos na horizontal seja 30 e a soma dos algarismos dispostos na vertical seja 22, qual é o algarismo que ocupará o lugar do X?

A)3
B)4
C)5
D)6
E)7

Para somar os dígitos de 1 a 9, pode-se somar as duas linhas abaixo em ordem inversa:
Linha A: 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9
Linha B: 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1
A + B = 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 10
A + B = 9 * 10
A + B = 90
A soma de 1 a 9 é igual a metade do resultado, já que a sequência foi somada duas vezes.
Lina A = 45.

Na horizontal deve constar 30 e na vertical 22. Somando ambos:
30 + 22 = 52.

Veja que o número X se repete, pois faz parte da horizontal e da vertical. A dupla contagem desse número é que faz a diferença entre a soma dos dígitos (45) e a soma das linhas horizontal e vertical (52):
52 - 45 = 7

---

14) Utilizou-se 1311 dígitos para numerar as páginas de um livro a partir do número 1.
O número total de páginas do livro é
A) 189.
B) 433.
C) 473.
D) 533.

Para as páginas de 1 a 9 usam-se 9 dígitos.
Para as páginas entre 10 e 99 usam-se 2 dígitos por página, como há 90 páginas, ao todo são 180 dígitos.
A partir da página 100 usa-se 3 dígitos por página.
1311 - 189 = 1122 dígitos restantes
1122 / 3 = 374 páginas de três dígitos, incluindo a página número 100.
Ao todo, o livro tem 99 + 374 = 473 páginas.

---

15) Em um arquivo há 750 fichas com dados de alunos de uma escola. Um terço das fichas são de crianças com até 7 anos de idade; metade das fichas de crianças com idade acima de 7 anos até 10 anos. O número de fichas de crianças com mais de 10 anos de idade é
A) 375.
B) 250.
C) 150.
D) 125.

Um terço de 750 é igual a 250 fichas de crianças com até 7 anos de idade.
A metade de 750 é 375 fichas que pertencem à crianças com idade acima de 7 e menor ou igual a 10.
750 - 250 - 375 = 125 restantes que comtêm dados das crianças acima de 10 anos.

---

16) Uma pessoa utilizou 2/9 de seu salário líquido para comprar um aparelho de TV, e 3/7 do restante foram utilizados em pagamentos de contas, sobrando ainda R$ 1.600,00. O preço pago no aparelho de TV foi
A) R$ 750,00.
B) R$ 800,00.
C) R$ 830,00.
D) R$ 880,00.
E) R$ 900,00

Salário igual a x.
Após utilizar 2/9 de x sobraram 7/9 de x, vamos chamar esse valor restante de y.
Após utilizar 3/7 de y sobraram 4/7 de y que equivale a 1600 reais.

(4/7)y = 1600
y = (7/4)1600
y = (7)400
y = 2800

(7/9)x = y
(7/9)x = 2800
x = (9/7)2800
x = (9)400
x = 3600.

O aparelho de TV custou 2/9 de x, isto é, R$ 800,00.

---

17) (2008 - FCC) Na representação de um número no sistema decimal de numeração são usados os algarismos de 0 a 9, de forma que cada dígito do número é o produto de seu valor nominal e a apropriada potência de 10, relativamente à posição do dígito no número. Assim, por exemplo,
[tex]7028=7*10^{3}+0*10^{2}+2*10^{1}+8*10^{0}[/tex]
Considerando que na Matematicolândia – país em que todos amam a Matemática – é usado somente um sistema numérico de base k, sabe-se que Esli, um de seus habitantes, comprou em certa loja um artigo por 240 u.m. (unidades monetárias) e usou uma cédula de 401 u.m. para pagá-lo. Se, após essa transação, Esli recebeu 111 u.m. de troco, o preço de tal artigo equivale, no Brasil, a
A) R$ 60,00
B) R$ 64,00
C) R$ 70,00
D) R$ 82,00
E) R$ 86,00

401 em base k equivale a [tex]4*k^{2}+0*k^{1}+1*k^{0}=\mathbf{4k^{2}+1}[/tex];
240 em base k equivale a [tex]2*k^{2}+4*k^{1}+0*k^{0}=\mathbf{2k^{2}+4k}[/tex] e
111 em base k equivale a [tex]1*k^{2}+1*k^{1}+1*k^{0}=\mathbf{k^{2}+k+1}[/tex].

Então,
[tex]401_{k} - 240_{k} = 111_{k}[/tex]

[tex]4k^{2}+1-(2k^{2}+4k)=k^{2}+k+1[/tex]

[tex]4k^{2}+1-2k^{2}-4k=k^{2}+k+1[/tex]

[tex]4k^{2}-2k^{2}-k^{2}-4k-k+1-1=0[/tex]

[tex]k^{2}-5k=0[/tex]

[tex]k(k-5)=0[/tex]

[tex]k=5[/tex]

Portanto, o preço do artigo no Brasil é:
[tex]240_{k}=2k^{2}+4k[/tex]

[tex]240_{5}=2(5)^{2}+4(5)[/tex]

[tex]240_{5}=2(25)+20[/tex]

[tex]240_{5}=70_{10}[/tex]

O artigo custa 70 reais.

---

18) (2013 - FCC) A soma S é dada por:
[tex]S=\sqrt{2}+\sqrt{8}+2\sqrt{2}+2\sqrt{8}+3\sqrt{2}+3\sqrt{8}+4\sqrt{2}+4\sqrt{8}+5\sqrt{2}+5\sqrt{8}[/tex]

A) [tex]\sqrt{90}[/tex]
B) [tex]\sqrt{405}[/tex]
C) [tex]\sqrt{900}[/tex]
D) [tex]\sqrt{4050}[/tex]
E) [tex]\sqrt{9000}[/tex]

Resposta envolve apenas algebra.
[tex]S=\sqrt{2}+\sqrt{8}+2\sqrt{2}+2\sqrt{8}+3\sqrt{2}+3\sqrt{8}+4\sqrt{2}+4\sqrt{8}+5\sqrt{2}+5\sqrt{8}[/tex]

[tex]S=(1+2+3+4+5)\sqrt{2}+(1+2+3+4+5)\sqrt{8}[/tex]

[tex]S=15\sqrt{2}+15\sqrt{8}[/tex]

[tex]S=15\sqrt{2}+15\sqrt{4*2}[/tex]

[tex]S=15\sqrt{2}+30\sqrt{2}[/tex]

[tex]S=45\sqrt{2}[/tex]

[tex]S=\sqrt{45^{2}*2}[/tex]

[tex]S=\sqrt{45*45*2}[/tex]

[tex]S=\sqrt{90*45}[/tex]

[tex]S=\sqrt{4050}[/tex]

---

19) (2012 - CESGRANRIO)São dados dois números x e y. Sabe-se que, se x ≤ y, então y > 3, e, se y < x, então x < 5. Portanto, se 2 + y = x, tem-se:
A) y < 3
B) y > 7
C) y = 5
D) x > 5
E) x = 5

A equação final, 2 + y = x, nos informa que x > y, pois é necessário acrescentar duas unidades a y para se igualar a x.
Como x > y, segue que x < 5, conforme diz o enunciado.
Como 2 + y = x e como x < 5, conclui-se que 2 + y < 5. Ou seja, y < 3.

---

20) Com duas letras iguais a X e n letras iguais a Y são obtidos 21 anagramas. Qual é o valor de n?
A) 4
B) 5
C) 6
D) 7
E) 8

Acredito que a forma mais ligeira seja testar as alternativa uma por uma.
Para fins didáticos, segue uma solução usando a fórmula de permutação com elementos repetidos:

---

21) Gustavo deve distribuir 4 livros diferentes para 8 crianças, de modo que uma ou mais crianças não recebam livro nenhum, podendo ocorrer de uma ou mais crianças receberem mais de um livro. O número de maneiras como ele pode distribuir os livros é igual a
A) 3488
B) 3682
C) 3854
D) 3962
E) 4096

Você tem quatro livros para distribuir entre oito estudantes.
Eu acho que a forma fácil consiste em associar o nome de um estudante a cada um dos livros.
Ou seja, o primeiro livro pode ficar com qualquer um dois oito.
O segundo livro pode ficar com qualquer um dois oito.
O terceiro livro pode ficar com qualquer um dois oito.
E o quarto livro também.
Associando essas 4 possibilidades, chega-se a um arranjo com repetição:
Arep(8,4) = 8 * 8 * 8 * 8
Arep(8,4) = 8^4
Arep(8,4) = 4096.

---

22) Uma empresa possui 20 funcionários, dos quais 10 são homens e 10 são mulheres. Desse modo, o número de comissões de 5 pessoas que se pode formar com 3 homens e 2 mulheres é:
A) 5400
B) 165
C) 1650
D) 5830
E) 5600


120 * 45 = 4.500

---

23) (ESAF) Um crime foi cometido por uma e apenas uma pessoa de um grupo de cinco suspeitos: Armando, Celso, Edu, Juarez e Tarso. Perguntados sobre quem era o culpado, cada um deles respondeu:
Armando: "Sou inocente"
Celso: "Edu é o culpado"
Edu: "Tarso é o culpado"
Juarez: "Armando disse a verdade"
Tarso: "Celso mentiu"

Sabendo-se que apenas um dos suspeitos mentiu e que todos os outros disseram a verdade, pode-se concluir que o culpado é:
A) Armando
B) Edu
C) Celso
D) Juarez
E) Tarso

Assuma que todos falam a verdade.
Como Celso e Edu acusam outra pessoas, fica claro que um dos dois está mentindo.
Sendo que um dos dois está mentindo, então Tarso está dizendo a verdade.
Celso é o mentiroso.
Logo, Tarso é o criminoso.

---

Um jovem, ao ser flagrado no aeroporto portando certa quantidade de entorpecentes, argumentou com os policiais conforme o esquema a seguir:

Premissa 1: Eu não sou traficante, eu sou usuário;
Premissa 2: Se eu fosse traficante, estaria levando uma grande quantidade de droga e a teria escondido;
Premissa 3: Como sou usuário e não levo uma grande quantidade, não escondi a droga.
Conclusão: Se eu estivesse levando uma grande quantidade, não seria usuário.

Considerando a situação hipotética apresentada acima, julgue os itens a seguir.

24) A proposição correspondente à negação da premissa 2 é logicamente equivalente a “Como eu não sou traficante, não estou levando uma grande quantidade de droga ou não a escondi”.

Trata-se de uma afirmação do consequente (falácia non sequitur).
Poder-se-ia concluir que ele não é traficante pelo fato dele não estar levando uma grande quantidade de droga e não a ter escondido. Não é possível concluir nada a partir dele não ser traficante.
Premissa 2: T → (G ^ E)
Equivale a: ~(G ^ E) → ~T
Equivale ainda a: (~G v ~E) → ~T
Assertiva 46 diz que: ~T → (~G v ~E) (inverteu a ordem dos acontecimentos)
Falso.

---

25) Sob o ponto de vista lógico, a argumentação do jovem constitui argumentação válida.

O enunciado poderia ser reescrito assim:
Premissa 1: ~T
Premissa 2: T → (G ^ E)
Premissa 3: (~T ^ ~G) → ~E
Conclusão: G → T
G não é condição suficiente para ser traficante em nenhuma das premissa. A conclusão é inválida, pois não decorre das premissas.
Falso.

---

26) Com os algarismos 1,2,3,4,5 e 6 sem repeti-los, podemos escrever "X" números de 4 algarismos, maiores que 3.200. O valor de 'X' é:
A)210
B)228
C)240
D)300
E)320

Você pode escrever A(6,4) números com esses algarismos.
A(6,4) = 6! / (6-4)! = 6*5*4*3 = 360 números distintos.

Porém você não pode escrever números que comecem com os algarismos 1XXX, 2XXX ou 31XX.
1XXX = 1 * A(5,3) = 60 números distintos,
2XXX = 1 * A(5,3) = 60 números distintos,
31XX = 1 * A(4,2) = 12 números distintos.

Ao todo: 360 - 60 - 60 - 12 = 228 números.

---

27) Dois reservatórios A e B têm a forma de um paralelepípedo, com bases quadradas de arestas internas iguais a 2 m e 3 m, respectivamente. Inicialmente o reservatório A tem 3,25 m a mais de altura de coluna de água do que o reservatório B. Para que os dois reservatórios fiquem com a mesma altura de coluna de água, deve ser passado do reservatório A para o reservatório B um volume de água, em litros, igual a
A) 9000.
B) 7750.
C) 6500.
D) 4000.
E) 3250.

Área do piso do reservatório A = 2m * 2m = 4m²
Área do piso do reservatório B = 3m * 3m = 9m².

O volume total de água nos reservatórios não nos interessa.
O que interessa é o volume de água acima da linha vermelha, pois é água desse volume que será transferido de A para B.

Volume de água em A acima da linha vermelha = área da base de A * altura da água acima da linha vermelha
Volume de água = 4 m² * 3,25 m
Volume de água = 13 m³
V(A) = 13 m³

Como inicialmente não há água acima da linha vermelha no reservatório B:
V(B) = 0 m³

Uma parte, X, desses 13 m³ de A deve ser transferida para o reservatório B de modo que os níveis de água fiquem iguais.
Nível de água de A inicial = Volume / área
Nível de água de A final = (Volume - X) / área
N(A) = (13 - X) / 4

Nível de água de B inicial = Volume / área
Nível de água de B final = (Volume + X) / área
N(B) = (0 + X) / 9

N(A) = N(B)
(13 - X)/4 = X / 9
9(13 - X) = 4X
117 - 9X = 4X
13X = 117
X = 9 m³ ou 9.000 L

---

28) (CESGRANRIO) Quantos números naturais de 5 algarismos apresentam dígitos repetidos?
A)27.216
B)59.760
C)62.784
D)69.760
E)72.784

É mais fácil contar o número de algarismos com dígitos distintos. Os algarismos que não têm todos os dígitos distintos, têm portanto pelo menos 2 dígitos iguais.

Total de números com cinco algarismos:
Entre 0 e 99.999 há 100.000 números.
Entre 0 e 9.999 há 10.000 números.
Então entre 10.000 e 99.999 há 90.000 números.

Total de números com cinco algarismos distintos:
O lance do problema é que a casa da dezena de milhar não pode ser igual a zero.
O número 01.234 não é válido.
No primeiro algarismo temos as opções: 1, 2, 3, 4, 5, 6, 7, 8, e 9. São nove opções:
9 * _ * _ * _ * _

No segundo algarismos temos as opções de 0 a 9, exceto o dígito que foi usada na primeira casa:
9 * 9 * _ * _ * _

No terceiro algarismos temos as opções de 0 a 9, exceto os dígitos que foram usado nas duas primeiras casas:
9 * 9 * 8 * _ * _

Seguindo essa lógico, temos 7 opções para o quarto algarismo e 6 para o último.
9 * 9 * 8 * 7 * 6 = 27.216

Total de números com pelo menos dois algarismos repetidos = 90.000 - 27.216 = 62.784.

---

29) Quantos anagramas de 5 letras distintas podem ser formados com as letras T,R,A,N e S se o R não pode preceder o T?
A)24
B)48
C)60
D)84
E)120

Pode-se deduzir pela simetria das permutações que o números de vezes em que o R precede o T é o mesmo número de vezes em que o T precede o R.
Logo, ao todo existem P(5) = 5! = 120 permutações possíveis e na metade delas (60) o R estará à frente do T.

---

30) Considere a seguinte sequência de figuras

Se a 21ª figura é formada por 881 bolinhas, então o número de bolinhas necessárias para formar a 22ª figura é
A) 1060
B) 1013
C) 986
D) 968
E) 925

Note que o número de bolinhas na aresta maior de cada figura é sempre um número ímpar em sequência. A primeira figura possui uma bolinha na areata, a segunda possui três bolinhas na aresta maior, a terceira figura possui cinco bolinhas na aresta maior e assim por diante.
Uma regra geral pode ser criada para calcular o número de bolinhas na aresta maior:
y = 2x - 1, em que y é o número de bolinhas e x é o índice da figura.
Por exemplo, para a quinte figura há:
y = 2(5) - 1
y = 10 - 1
y = 9 bolinhas na aresta maior.

Se as figuras não tivessem um vazio no meio, o número de bolinhas seria igual a fórmula da área de uma quadrado, ou seja, y vezes y.
Note que o espaço vazio de cada figura é preenchido pela figura anterior.
Tome por exemplo as figuras 3 e 4. Obtém-se a figura a seguir quando se insere a 3ª sequência na 4ª:

O número de bolas nessa figura é igual 49, que seria a área da figura 4 caso não houvesse espaço vazio.
O mesmo se aplica a 22ª figura.
Primeiro, é necessário encontrar o número de bolas na aresta da figura 22 para calcular a área.
y = 2x - 1
y = 2(22) - 1
y = 44 - 1
y = 43

A área da figura 22, sem levar em consideração o espaço vazio, é igual a 43*43 = 1849.
O espaço vazio será igual à figura anterior, que o enunciado informa ter 881 bolinhas.
Logo, a figura 22 tem 1849 - 881 = 968 bolinhas e a letra D responde à questão.